Accuracy:

Clock accuracy is largely determined by how well we can characterize the electromagnetic environment and the sensitivity of the atomic transition to these disturbances. In addition, motion of the atom introduces relativistic corrections. The most fundamental influences on clock accuracy for an ion-based clock are:

  • Thermal motion: Residual motion of the atom gives rise to a second order Doppler shift, also called the time dilation shift as it arises from relativistic corrections. It is inversely proportional to the mass of the atom, which favors heavier atoms such as lutetium.
  • Magnetic fields: Energy levels shift in the presence of a magnetic field, an effect known as the Zeeman effect. Linear shifts are readily cancelled by averaging over multiple transitions. Quadratic shifts arise from coupling to other levels and diminish with increasing energy separations.
  • Probe fields: The probe laser itself induces an AC Stark shift proportional to the dynamic scalar polarizability at the clock frequency Δα0(ω0) and the laser intensity. This is more significant for clock transitions having very long lifetimes as higher intensity is needed to drive the transition.
  • Blackbody radiation (BBR): Thermally generated electric fields cause an AC-Stark shift that scales with the 4th power of temperature and proportional to the static differential scalar polarizability, Δα0(0).
  • Tensor shifts:
    • Quadrupole and tensor polarizability shifts appear when the electronic angular momentum J>1/2. Quadrupole shifts arise from coupling of the atom to gradients of the electric field. Gradient fields are often used to confine the ion and are also generated by any nearby ions. The tensor polarizability, determines the dependence of the AC-Stark shift on the orientation of the electric field relative to the magnetic field.
  • Micromotion:
    • Rapid small amplitude motion driven by the rf fields confining the ion, gives an AC-Stark shift and a second order Doppler shift. If Δα0(0)<0, the two shifts have opposite sign and can be made to cancel when the trap drive field frequency, Ω0, has a specific value, which we dub the magic rf frequency.

    Stability:

    Rabi spectroscopy is a common method for probing or interrogating an atomic transition: the laser drives the atomic transition for a time T and then population in the excited state is measured. The resulting frequency dependent signal is shown here for assuming the laser intensity is such that population transfer is a maximum when the laser is on resonance. The signal has a height determined by the number of atoms, N, and a width inversely proportional to T.

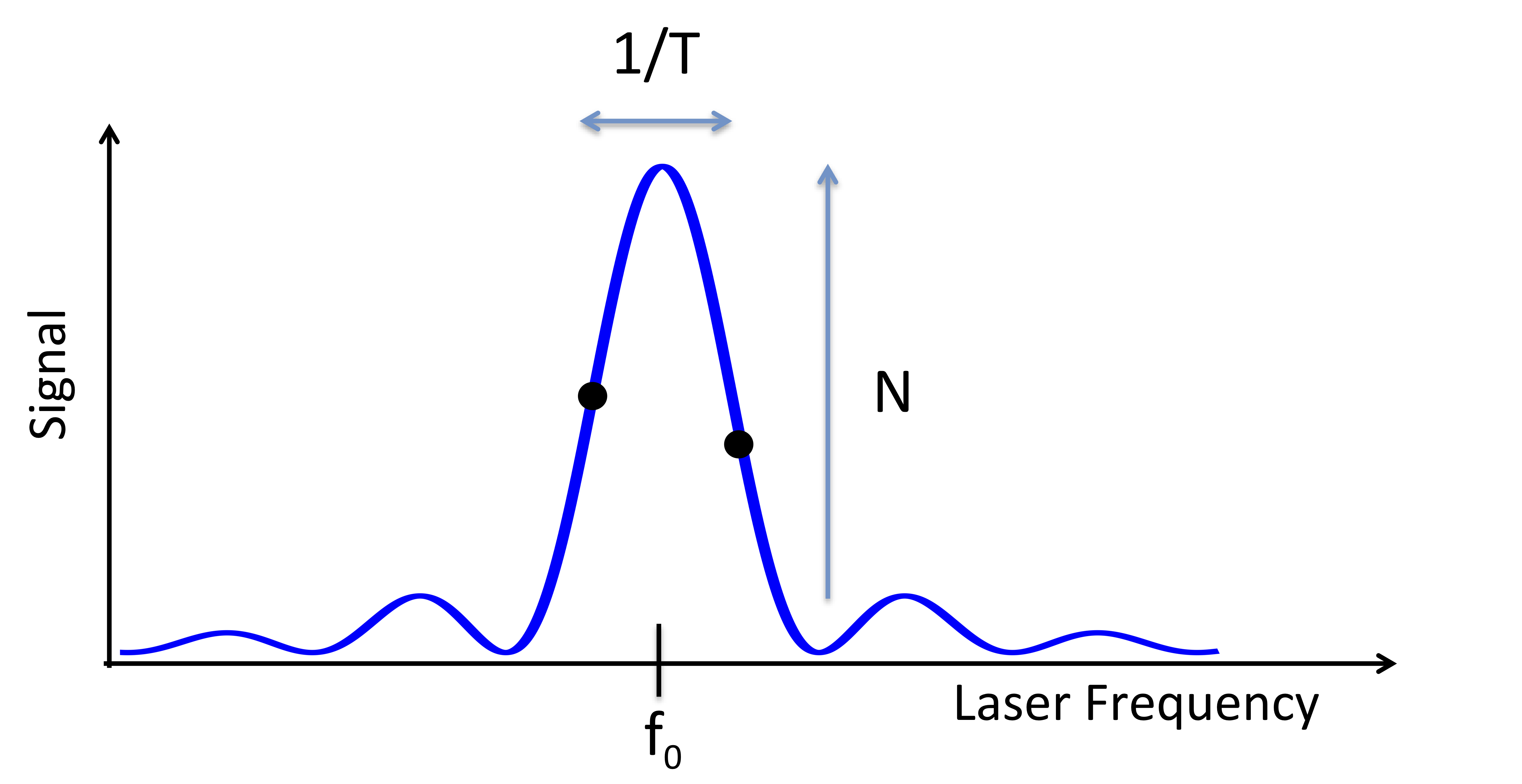
    In clock operation, the atom is probed either side of the resonance and the difference in the two signals is used to derive an error signal from which to correct the laser frequency. At the half maximum point an atom has a 50% chance of being found in the excited state and hence the error signal has a projection noise of , resulting a frequency variation of . In a time τ we can ideally make τ/T measurements resulting in a fractional instability

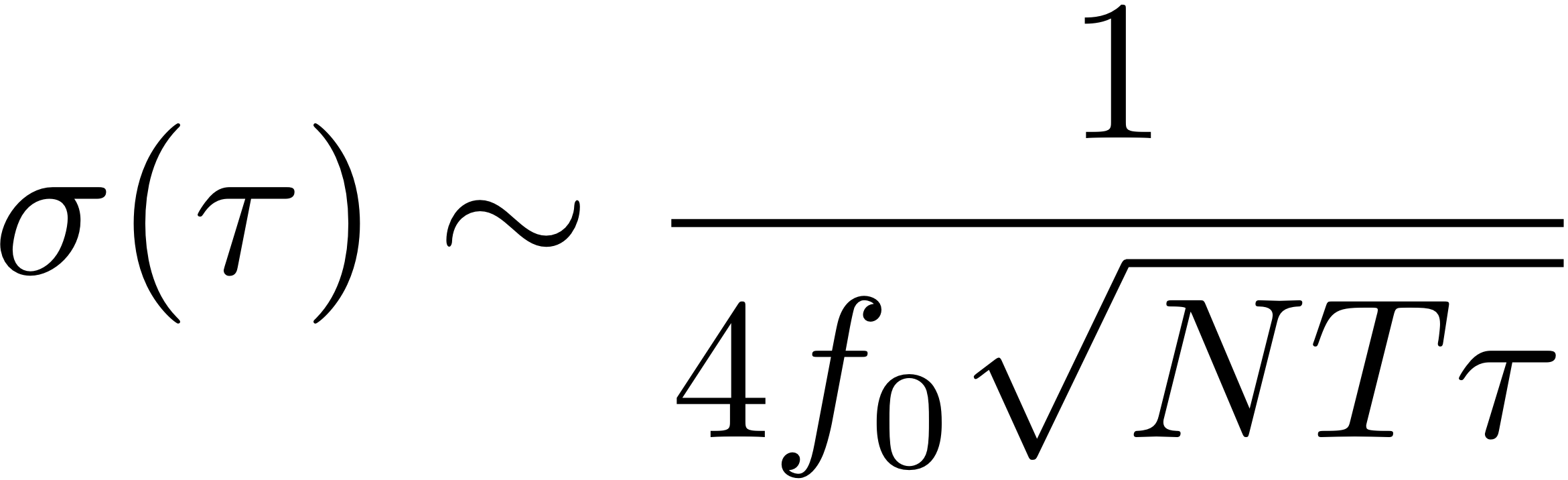
    Other interrogation techniques, such as Ramsey spectroscopy, yield a similar result. This expression motivates the use of higher clock frequencies, larger numbers of atoms and longer interrogation times.

    The interrogation time T is limited by the transition lifetime, environmental noise shifting the atomic transition, or the laser coherence time. We typically choose transitions that have long lifetimes and low sensitivity to external noise so that, in practice, the limitation is due to laser technology.